A few days ago someone asked, if there is a way, to generate random numbers in a CL program or procedure.

Of course it would be a lot easier to use embedded SQL and the RANDOM() function in RPG or COBOL, but he explicitly wanted CL. He needed (pseudo) random numbers between 1 and 1000.

IBM i has a suite of crypto APIs – and one of them is QC3GENRN (or Qc3GenPRNs in ILE) to generate pseudo random binary data. The prototype for the API in RPG looks like this:

/include qsysinc/qrpglesrc,qusec
 
dcl-pr QC3GENRN extpgm('QC3GENRN');
  prnData char(1000) options(*varsize); 
  prnDataLen int(10:0) const;
  prnType char(1) const;
  prnParity char(1) const;
  errorCode likeds(qusec);
end-pr;

• prnData – output – the „resulting“ pseudo random binary data after the API call
• prnDataLen – input – how many bytes of pseudo random data should be created
• prnType – input
  • ‚0‘ = generate real pseudo random data
  • ‚1‘ = generate test data with preset values for key and seed
• prnParity – input
  • ‚0‘ = do not use parity
  • ‚1‘ = set each byte to odd parity
  • ‚2‘ = set each byte to even parity
• errorCode – input/output – the usual QUSEC errorCode data structure, which in the simpliest form is structured like this
  • int(10:0) – input – size of the provided data structure – if this is set to zero, no exception id is returned, and the exception is sent to the calling program – in the simplest form you can just use an 4-byte integer variable with value zero instead of a real data structure
  • int(10:0) – output – bytes of data available after the call
  • char(7) – output – the exception id (message id like ‚CPF1234‘)
  • char(1) – output – reserved
  • char(*) – output – exception message data

So how is this API callable from CL? Lets see the code:

The parameters and the call to QC3GENRN is pretty straight forward. After the call, we have 4 bytes of pseudo random binary data in the &data variable. To use that data, we have to convert it first.

1. We use %binary(...) to convert the binary data to a number – 4 bytes means, we can use a 4 byte integer.
2. Integer variables are signed – so we can receive negative values – if the value is below zero, we multiply with -1, because CL has no absolute function like SQL or RPG
3. We wanted numbers between 1-1000, and because CL also has no modulus or remainder function, we need to do that by integer dividing by 1000 …
4. … and subtraction the result multiplied with 1000 from our original number. The remainder should now be a number between 0 and 999.
5. So in the last step we add 1 to the remainder and we have numbers between 1 and 1000.

I hope you will find this little experiment useful, and of course I appreciate your comments.

P.S.: Here is the code ready for copy and paste:

pgm

/* QC3GENRN API parameters */
dcl var(&data) type(*char) len(4)  value('    ')
dcl var(&datalen) type(*int) len(4)  value(4)
dcl var(&type) type(*char) len(1)  value('0')
dcl var(&parity) type(*char) len(1)  value('0')
dcl var(&qusec) type(*int) len(4)  value(0)

/* some working vars */
dcl var(&work1) type(*int) len(4) value(0)
dcl var(&work2) type(*int) len(4) value(0)

/* result - random number 1-1000 */
dcl var(&random) type(*dec) len(4 0) value(0)

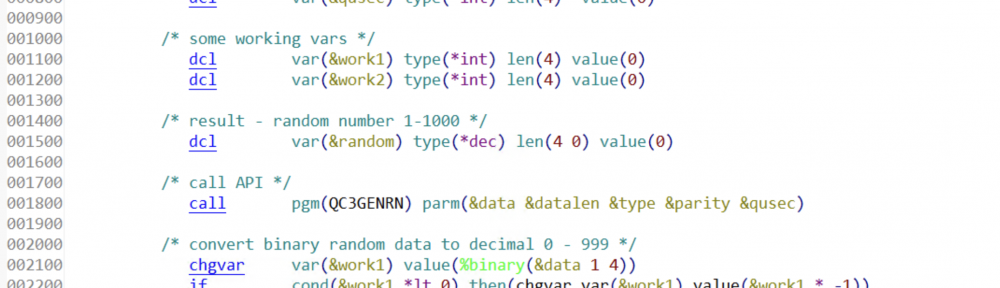
/* call API */
call pgm(QC3GENRN) parm(&data &datalen &type &parity &qusec)

/* convert binary random data to decimal 0 - 999 */
chgvar var(&work1) value(%binary(&data 1 4))
if cond(&work1 *lt 0) then(chgvar var(&work1) value(&work1 * -1))
chgvar var(&work2) value(&work1 / 1000)
chgvar var(&work1) value(&work1 - (&work2 * 1000))

/* set result variable to range 1 - 1000 */
chgvar var(&random) value(&work1 + 1)

endpgm